WaveFunctionCollapse is Constraint Solving in the Wild

WaveFunctionCollapse has continued to be one of the more interesting new procedural generation algorithms. People have been finding all kinds of things to use it for: minigolf courses, 3D maze buildings, poetry, and animations.

But people are still having trouble understanding how it works. While you can use one of the existing implementations and get perfectly good results, if you want to extend the algorithm or apply it to new contexts it’s been hard going. That’s one reason I co-wrote this research paper on how WFC works.

Section 4 is a walk-through of the algorithm. Starting from one 4x4 pixel image, you can see the steps it goes through. The image is broken down into patterns, cataloging each unique sub-image:

We build a catalog of the different ways these patterns can overlap. With a 2x2 pattern size, there are nine ways that can happen:

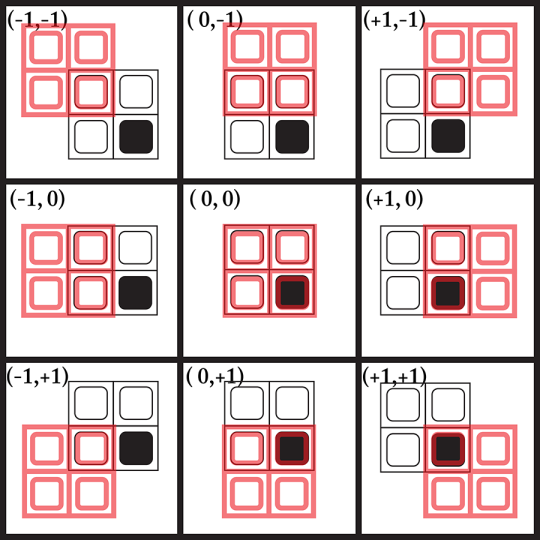
Here’s what that index catalog looks like for the first pattern, the one with three white pixel and one black pixel in the lower right corner:

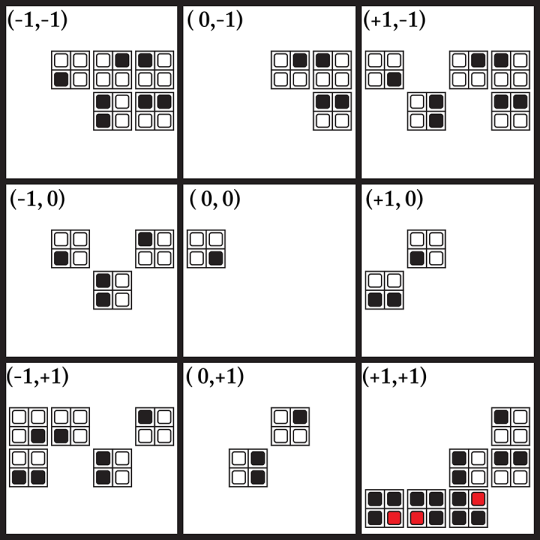
At (0,0) in the center are all the patterns that exactly overlap with this one. There’s only one, of course: itself. If we instead look at the patterns that only overlap with the two pixels on the right, shown at (+1, 0), there are two patterns that fit: one with two black pixels in the bottom row, and one with a black pixel in the lower left.

With pattern sizes larger than 2x2 things quickly get more complicated: 3x3 has 25 ways to overlap, 4x4 has 36 ways to overlap, and so on. Because we only care about unique patterns this takes less space to store than it might seem, but it still gets hard to visualize.

Note, also, the structure that this imposes on the output: a red pixel can never be next to a white pixel, because there are no pattern overlaps that allow that. This is how things like the Flower WFC example work: the flower must be at the top of a green stem and surrounded by blue sky, because those are the only valid matches for the yellow petals.

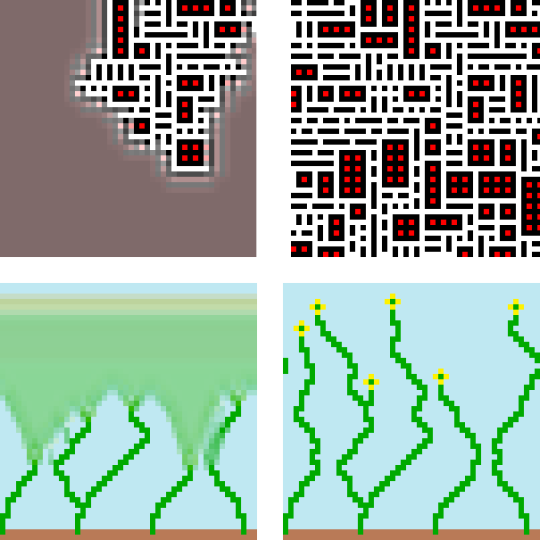
Moreover, since the 3x3 Flower patterns only have blue sky above them, the top two rows of the output will always be blue, even though the WFC code has no explicit constraints for the top rows.

With the index catalog in hand, the algorithm looks at the current output and finds the point that has the lowest entropy–that is, the point where there are the fewest possible patterns that fit. This is called the Observation step. If there’s more than one possibility there, it picks one of them at random. That’s the only place where randomness comes into the algorithm.

After Observation comes Propagation: WFC checks how many patterns are still valid for other cells in the output. The effect of one cell being fixed affects the surrounding possibilities, and often a large area will suddenly cohere into the only remaining valid configuration.

That’s the basics of how it works. There’s more details in the paper itself, of course. If you’d like to know more I encourage you to read it and let me know if you found it helpful. Or if you have questions about it.

The paper isn’t just about how the algorithm works, of course. The paper covers the history of WFC, its relationship to other similar algorithms, and–perhaps most importantly for future research–a look at how WaveFunctionCollapse can be treated as a subset of constraint solving.

By implementing a surrogate for WFC in answer set programming, we can see that we can use the WFC propagator as the constraint and turn the problem into a logic program that can be solved with an automatic solver. (Clingo, in this case.)

This lets us do things like compare different heuristics and demonstrate the importance of the constraint propagation. The experiments show that the constraint propagation means that it can work without backtracking, and only the occasional global restart. Or without constraint propagation but with lots of backtracking.

It also makes it easy to introduce new constraints on top of the basic WFC constraints. The example we used in the paper is that all the patterns in the input must be present in the output, but that’s just one possibility among many. Perhaps we want all the red pixels to be connected in a single graph by a network of blue pixels. Or, for a more concrete example, if we want to generate a dungeon level, but have a constraint that you must be able to find a path from the entrance to the exit.

Again, there are many more details in the paper itself. The paper will be presented by Adam M. Smith, my co-author, and myself at the 2017 Procedural Generation Workshop this August.

http://isaackarth.com/papers/wfc_is_constraint_solving_in_the_wild/