Discovery of the Mandelbulb (2009)

The thing that makes Mandelbrot’s fractal feel so much like a natural phenomenon is that its mathematical representation is so simple. The familiar images are simply visualizations of coordinates of complex numbers, with the real part on the horizontal axis and the imaginary part on the vertical axis. For each pixel on the plane, calculate how rapidly the sequence diverges and color the pixel accordingly.

There’s no 3D equivalent to the complex number plane, so there’s no true three-dimensional Mandelbrot set. However, that hasn’t stopped artists and mathematicians from searching for formulas that yield 3D fractals with somewhat similar visual properties.

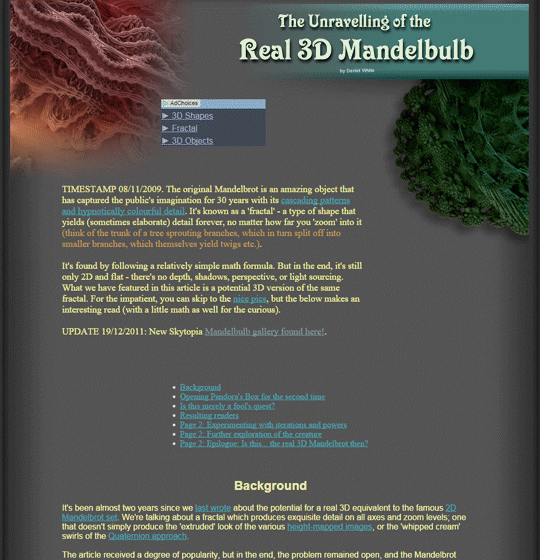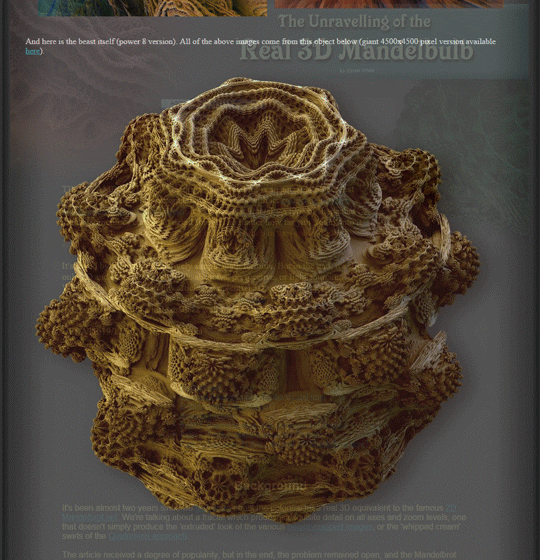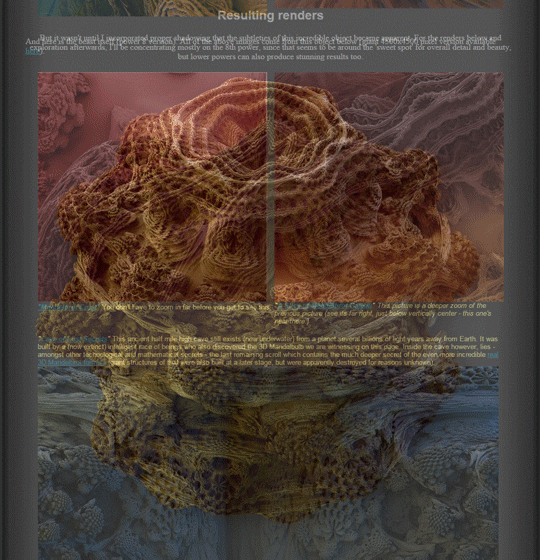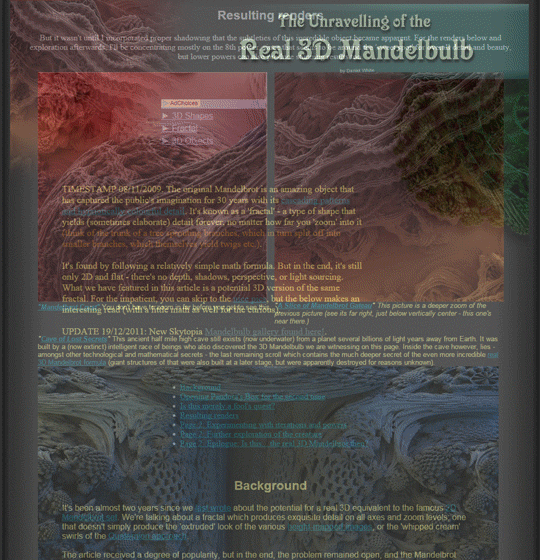
In 2009, Daniel White and Paul Nylander (plus the Fractal Forums community) found something that fit the bill, which they called the Mandelbulb. The formula uses spherical coordinates (instead of the 2D polar coordinates) and squaring part of the formula to a higher power (typically 8). The result is as close as we’ve come so far to being a three-dimensional representation of the Mandelbrot set.

Today, there are multiple software tools that can render the Mandelbulb and similar 3D fractal objects, and artists are continually finding new ways to view these mathematical intrusions into our home dimension. 

The explanation and story of the discovery are eloquently conveyed in Daniel White’s write-up: http://www.skytopia.com/project/fractal/mandelbulb.html